Vokiel.com

W życiu programisty pojawiają się sytuacje, gdy programowanie styka się bardzo blisko z matematyką, w tym przypadku z geometrią. We wpisie postaram się przedstawić sposób na rozwiązanie problemu przynależności punktu do obszaru wielokąta (opisanego przez zbiór wierzchołków).

Geofencing

Ostatnio mam dość mało czasu na pisanie na blogu. Jest to związane przede wszystkim z lenistwem, a w drugiej mierze z mojego udziału w jednym, ciekawym projekcie. Z owym projektem wiąże się dzisiejszy wpis. W aplikacji tej zaplanowaliśmy ciekawą funkcjonalność: geofencing, czyli ¹:

Geofencing is a term utilized primarily in the corporate world that refers to the practice of limiting mobile employees to a specific geographic location by tracking their whereabouts via the technology of a global positioning system (GPS).

W telegraficznym skrócie polega to na wyznaczeniu bezpiecznego obszaru, po którym może poruszać się urządzenie z zainstalowanym modułem GPS.

Zastosowań jest wiele, począwszy od śledzenia pracowników, po zabezpieczenia przesyłek. Przy wszystkich zastosowaniach pojawia się ta sama potrzeba sprawdzenia, czy raportowany z urządzenia GPS punkt znajduje się w obrębie zdefiniowanego obszaru, czy jest już poza nim. Możliwości sprawdzenia przynależności punktu do wielokąta jest wiele.

Przynależność do figury prostej

W najprostszym przypadku prostokąta sprowadza się do prostego, matematycznego porównania współrzędnych wierzchołków i sprawdzanego punktu. Nie wymaga skomplikowanych obliczeń, tym bardziej geometrycznych. Niestety sposób mało przydatny w realnym zastosowaniu. Kazać użytkownikom rysować prostokąty wzdłuż trasy Warszawa – Moskwa może kwalifikować się na nagrodę Worst UX. Dzielenie narysowanego skomplikowanego wielokąta na małe prostokąty, następnie sprawdzanie przynależności punktu do każdego z nich też nie wydaje się optymalnym rozwiązaniem.

Metody dla dowolnego wielokąta

Przeszukując otchłanie Internetu można napotkać rozważania nad różnymi metodami na rozwiązanie tego zagadnienia. Kilka z nich zebrał Eric Haines w artykule Point in Polygon Strategies. ²

Suma kątów

Ta metoda polega na zliczeniu sumy kątów liczonych od sprawdzanego punktu do poszczególnych wierzchołków z bokiem wychodzącym z tego wierzchołka. Jeśli suma tych kątów będzie bliska zeru to punkt będzie poza wielokątem, w przeciwnym wypadku będzie do niego należał. Niestety z powodu wykorzystania funkcji trygonometrycznych, konieczności wyznaczenia prostej od każdego wierzchołka do szukanego punktu i wyliczenia dla nich kątów, jest to metoda bardzo powolna.

 

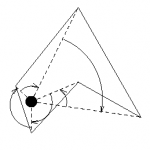
Metoda trójkątów

Kolejna, dość obciążająca metoda, polega na podzieleniu wielokąta na trójkąty składowe. Następnie sprawdza się dla każdego z tak utworzonych trójkątów, czy punkt leży w jego obrębie. Jeśli mamy do czynienia z wielokątem wypukłym pierwsze trafienie automatycznie przerywa proces sprawdzania. W celu przyśpieszenia algorytmu można posortować utworzone trójkąty względem wielkości powierzchni lub długości boków. Zwiększy to szansę na wcześniejsze trafienie dopasowania, zmniejszając przy tym liczbę powtórzeń pętli.
Dla wielokątów niewypukłych należy przejść przez wszystkie trójkąty, przy tym zliczyć trafienia. Jeśli ich liczba jest nieparzysta, oznacza to, że punkt zawiera się w obrębie figury.

 

BSP-tree

Za pomocą tej metody można opisywać wielokąty i szybko stwierdzać przynależność punktu. Proces tworzenia jest niestety dość wolny, zatem powinno się je stosować, gdy występuje sprawdzanie wielu punktów do jednego wielokąta ³.
Korzystając z tej metody bada się, po której stronie linii na której leży odcinek zapisany w węźle znajduje się testowany punkt. W zależności od tego sprawdza się lewe, bądź prawe poddrzewo. Badanie rozpoczyna się od korzenia. Procedura kończy się wraz z natknięciem się na puste wskazanie.

Test przecięć

Test przecięć był moim pierwszym (w zasadzie jedynym) pomysłem, który zrodził się w głowie w drodze do domu (jak zwykle jak jest pomysł, to nie ma go czym, jak i gdzie zapisać 🙁 ). Jak tylko dotarłem do domu przelałem idee na papier – ołówek i notes to ciągle najlepszy sposób na projektowanie;). W trakcie obmyślania sposobu pojawiło się kilka wątpliwości w specyficznych sytuacjach, bardziej skomplikowanych modelach. Po konsultacji z jednym z najlepszych programistów jakich znam, miałem zaplanowaną całość rozwiązania. Powstała przy tym seria rysunków na draw.to 😉 Jak zauważył Antonone, moje twierdzenie o Krzywej Jordana zostało już opisane.

W związku z tym postanowiłem sprawdzić czy istnieje już gotowe rozwiązanie w PHP. Takowego nie znalazłem, ale pojawiło się kilka artykułów, które pomogły mi zweryfikować moją metodę ^4 5 6.

Wielokąt wypukły

Jeśli mamy do czynienia z wielokątem wypukłym jest troszeczkę łatwiej. Wystarczy poprowadzić półprostą ze sprawdzanego punktu w wybranym kierunku do punktu położonego poza ostatnim, najdalej wysuniętym w tym kierunku, wierzchołkiem wielokąta. Następnie wystarczy policzyć ilość przecięć półprostej z bokami figury (rys. 2). Jeśli liczba ta będzie nieparzysta – punkt znajduje się wewnątrz wielokąta, jeśli parzysta lub jest równa 0 – punkt znajduje się poza wielokątem.

Dowolny wielokąt

W przypadku dowolnego wielokąta trzeba liczyć się z pojawieniem się figury wklęsłej (najprawdopodobniej takie będą pojawiały się najczęściej). Tutaj postępowanie jest trochę inne.

W pierwszej kolejności dobrze jest sprawdzić, czy sprawdzany punkt należy do jednego z boków lub wierzchołków figury. Jeśli nie, to należy poprowadzić półprostą, równoległa do którejś osi (np OX), poprowadzonej ze sprawdzanego punktu, do punktu położonego poza ostatnim, najdalej wysuniętym w kierunku grotu osi, wierzchołkiem wielokąta. Sprawdzany punkt będzie leżał wewnątrz wielokąta, jeśli przeprowadzona z niego półprosta przecina jego boki nieparzystą ilość razy.

Przy wielokątach wklęsłych należy rozpatrzyć kilka szczególnych przypadków:

Półprosta zawiera się w jednym z boków wielokąta

Może zdarzyć się, że przeprowadzona ze sprawdzanego punktu półprosta będzie przechodziła przez jeden z boków wielokąta (rys. obok). Przy sprawdzaniu zawierania się półprostej w odcinkach nastąpi wielokrotne mylne przyporządkowanie: półprosta przetnie odcinek A-B, B-C, C-D. Po głębszym zastanowieniu widzimy, że zliczanie tych przecięć nie ma sensu. Figura w tej sytuacji może dążyć do połączenia wierzchołków ponad wytyczoną półprostą lub przecinając ją. Jeśli połączy się ponad (tak jakbyśmy połączyli wierzchołki A-D) to szukany punkt będzie poza figurą. Jeśli połączy się pod, to punkt będzie w środku figury jednak będzie musiało nastąpić jeszcze przynajmniej jedno przecięcie półprostej z bokiem wielokąta.
Zatem w przypadku, gdy linie łączące się z odcinkiem, przez który przechodzi półprosta będą po jej jednej stronie liczba zliczonych przecięć będzie wynosiła zero.

 

W drugiej sytuacji (rys. obok), gdy linie przez które przechodzi półprosta będą po jej przeciwnych stronach zliczamy takie przecięcia jako jedno.
Tutaj podobnie jak powyżej, jeśli wierzchołki dążą do połączenia obejmując sprawdzany punkt w obręb wielokąta (w naszym przypadku po lewej stronie sprawdzanego punktu), to otrzymujemy nieparzystą liczbę przecięć. Jeśli natomiast złączą się poza punktem (w naszym przypadku po stronie grotu osi OX), to nastąpi przynajmniej jeszcze jedno przecięcie, zatem suma przecięć będzie parzysta – punkt poza wielokątem.

 

Półprosta przechodzi przez wierzchołek wielokąta

W ostatniej ewentualności półprosta przecina wierzchołek wielokąta. Podobnie jak wcześniej są dwie, możliwe do wystąpienia sytuacje. Pozostałe punkty boków wychodzących z przecinanego wierzchołka znajdują się po jej przeciwnych stronach (rys. 5) lub znajdują się po tej samej stronie (rys. 6).
W pierwszym przypadku liczymy jedno przecięcie pomimo, że punkt przechodzi przez dwa boki (A-B oraz B-C).
W drugim przypadku nie zaliczamy żadnego przecięcia.

Implementacja

Kiedy mamy już wszystko przemyślane, można przystąpić do implementacji rozwiązania w PHP. Jako, że ten wpis jest już i tak bardzo długi, rozwiązanie przeniosłem do kolejnego: Klasa PHP rozwiązująca problem przynależności punktu do wielokąta.

Źródła

1. http://www.wisegeek.com/what-is-geofencing.htm [↩]
2. http://erich.realtimerendering.com/ptinpoly/ [↩]
3. http://pl.wikipedia.org/wiki/Drzewo_BSP [↩]
4. Wojciech Muła – Reguła nieparzystości [↩]
5. Michał Knasiecki – Przynależność punktu do wielokąta [↩]
6. Janusz Ganczarski – Problem przynależności [↩]